Καθώς το trading σε live στοίχημα ποδοσφαίρου έχει γίνει δημοφιλές τελευταία, σκέφτηκα να δείξω τους υπολογισμούς του value για κάθε trade. Διότι ακόμα και στο trading σε ζωντανό στοίχημα υπάρχει το expected value, το προσδοκώμενο κέρδος που μακροχρόνια θα καταλήξει στο λογαριασμό του παίκτη – αν και συνήθως είναι προσδοκώμενη ζημία. Αναλύοντας την πιθανότητα να συμβεί το κάθε σενάριο κατά τη διάρκεια ενός αγώνα ποδοσφαίρου, εξετάζεται εάν τελικά το trade ήταν στο σύνολό του +EV ή –EV, εάν δηλαδή συνέφερε τον παίκτη ή όχι. Σπάνια οι παίκτες του στοιχήματος κάνουν τους παρακάτω υπολογισμούς, πόσο μάλλον σκέφτονται με αυστηρά μαθηματικό τρόπο. Εάν μέχρι τώρα δεν τα καταφέρνετε τόσο καλά στο ζωντανό στοίχημα, πιθανόν οι παρακάτω γραμμές σας βοηθήσουν να αντιστρέψετε την εις βάρος σας κατάσταση.
Για να γίνουν οι υπολογισμοί του expected value (EV) στο trading, πρέπει να υπάρχουν χειροπιαστά παραδείγματα. Για το λόγο αυτό θα αναφερθώ σε γραφήματα αποδόσεων live στοιχημάτων που έχουν δημοσιευτεί κατά καιρούς στο Online Στοίχημα.
Σενάριο 1: Ο Vasteras πετυχαίνει γκολ, οπότε σύμφωνα με το γράφημα η απόδοση πέφτει στο 1.3. Ο trader κλείνει τη θέση του εκεί με υπέρ στοίχημα.
Η πιθανότητα να συμβεί το παραπάνω σενάριο είναι θεωρητικά 71,4% (1 προς 1.40 ως μέση τιμή απόδοσης του στοιχήματος «επόμενο γκολ» ομάδας με απόδοση νίκης στο 1.70). Κλείνοντας τη θέση του o trader, το αρχικό του ρίσκο δεν είναι 70 ευρώ αφού το stop loss είχε ορισθεί στην επίτευξη γκολ του Vasteras. Παίζοντας υπέρ 131 ευρώ στο 1.30, πλέον βρίσκεται να χάνει 31 ευρώ ανεξαρτήτου αποτελέσματος. Το expected value σε αυτήν την περίπτωση είναι μείον 22,1 ευρώ (71.4% επί 31 ευρώ).
Σενάριο 2: Ο Vasteras δεν πετυχαίνει γκολ και ο αγώνας λήγει 0-0. Ο trader δεν κλείνει ποτέ τη θέση του.
Η πιθανότητα να συμβεί το παραπάνω σενάριο είναι θεωρητικά 10% (1 προς 10 ως μέση τιμή απόδοσης του ακριβούς σκορ 0-0). Το expected value αυτού του σεναρίου προκύπτει ίσο με 10 ευρώ (10% επί 100 ευρώ).
Σενάριο 3: Ο Vasteras δέχεται γκολ οπότε υποθέτοντας πως η απόδοσή του θα ανέβαινε στο 3 (αυθαίρετη υπόθεση). Ο trader κλείνει τη θέση του με υπέρ στοίχημα στο 3.
Η πιθανότητα να συμβεί το σενάριο αυτό είναι το υπολοιπόμενο ποσοστό από τα προηγούμενα σενάρια, δηλαδή 18.6%. Εφόσον υπάρχει 10% να μην μπει κανένα γκολ και 71.4% να επιτευχθεί το πρώτο γκολ από τον Vasteras, η μόνη άλλη πιθανή περίπτωση είναι να επιτευχθεί το πρώτο γκολ από την Hammarby. Ο trader κλείνει με υπέρ στοίχημα 57 ευρώ στο 3.00, εξασφαλίζοντας 44 ευρώ κέρδος ανεξαρτήτου αποτελέσματος. Αυτό σημαίνει πως το expected value είναι 8,18 ευρώ (44 ευρώ επί 18.6%).
Συγκεντρωτικά έχουμε:
Σύνολο +EV = 10 + 8,18 = 18,18
Σύνολο –EV = 22.1
EV = -3,92 ευρώ.
Άρα το παραπάνω trading του live στοιχήματος μεταξύ Hammarby και Vasteras είναι –EV, δηλαδή ασύμφορο για τον παίκτη. Πότε το trading του [intlink id=”6″ type=”category”]ζωντανού στοιχήματος[/intlink] που περιγράφηκε παραπάνω μπορεί να γίνει συμφέρον προς τον παίκτη; Ο μόνος παράγοντας EV που μπορεί να μεταβληθεί με τα υπάρχοντα δεδομένα είναι η απόδοση για νίκη του Vasteras εφόσον πετύχει τέρμα η Hammarby. Θα πρέπει ο trader να κερδίσει τουλάχιστον 3.92 ευρώ ώστε να μηδενίσει το τελικό συγκεντρωτικό EV. Εάν λοιπόν αντί για 3, η απόδοση τελικά ανέβει στο 5, το expected value του trader ανεβαίνει στα 12.28 ευρώ (66 ευρώ επί 18.6%) αφού κλείνοντας με 34 ευρώ υπέρ στο 5.0 θα έχει εξασφαλίσει κέρδος 66 ευρώ σε οποιοδήποτε αποτέλεσμα. Σε σύγκριση με τα 8.18 ευρώ του 3ου σεναρίου, έχει κερδίσει 4.1 ευρώ EV οπότε πλέον το trading κρίνεται οριακά ως κερδοφόρο μακροχρόνια (EV = 0.18ευρώ).
Διαπιστώνεται λοιπόν πως ενώ ο παίκτης ρίσκαρε φαινομενικά 70 ευρώ για πιθανό κέρδος 100 ευρώ, τελικά το καθαρό μακροχρόνιο κέρδος του είναι μόλις 0.18 ευρώ! Πριν αποφασίσουμε να κάνουμε trading σε [intlink id=”24″ type=”category”]live στοίχημα ποδοσφαίρου[/intlink] ή οποιουδήποτε άλλου αθλήματος θα πρέπει να σκεφτούμε τα παρακάτω βήματα:
- Σε ποια απόδοση θα κλείσουμε με ζημία το στοίχημά μας και εάν αυτή η απόδοση είναι εφικτή. Με άλλα λόγια εάν ορίζαμε το [intlink id=”1696″ type=”post”]stop loss[/intlink] στο παραπάνω παράδειγμα στο 1.5, είναι προφανές ότι κάτι τέτοιο δε θα ήταν δυνατό να συμβεί, αφού η απόδοση έπεσε στο 1.3 κατευθείαν.
- Ποια είναι όλα τα πιθανά σενάρια του αγώνα και της εξέλιξης των αποδόσεων.
- Ποια είναι η πιθανότητα να συμβεί το κάθε σενάριο.
- Πού θα βρεθούν οι αποδόσεις των στοιχημάτων σε κάθε τέτοιο σενάριο. Εδώ φυσικά είναι πολύ σημαντική η καταγραφή στατιστικών στοιχείων παρελθόντων αγώνων, ώστε να γνωρίζουμε εξαρχής πως θα κινηθούν οι αποδόσεις.
- Πόσα χρήματα θα χάσουμε ή θα κερδίσουμε σε κάθε σενάριο.
- Υπολογίζουμε το expected value πολλαπλασιάζοντας το πιθανό κέρδος ή ζημία για κάθε σενάριο επί την πιθανότητα του σεναρίου. Δηλαδή:
Όπου:
Π = πιθανότητα%
Κευρώ = Κέρδος σε ευρώ
Ζευρώ = Ζημία σε ευρώ
Σ = σύνολο των γινομένων όλων των πιθανών σεναρίων που είναι στην πρώτη μεταβλητή τα σενάρια με +EV και στη δεύτερη τα σενάρια με –EV.
χ= Σενάρια με +EV
ψ= Σενάρια με –EV
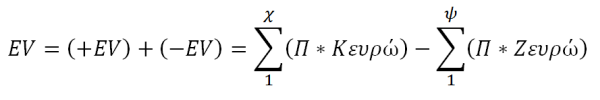
2 Comments
ΕΙΜΑΙ Ο ΜΟΝΟΣ ΠΟΥ ΔΕΝ ΚΑΤΑΛΑΒΕ ΤΙΠΟΤΑ? :P
Στην ουσία υπολογίζεις τη μέση τιμή της μεταβλητής Κ=κέρδος. Ισχύει P(Κ=-31€)=71.4%, P(K=+100€)=10% και P(K=+44€)=18.6%. Οι πιθανότητες αθροίζουν στο 1, άρα με βάση τον ορισμό της μέσης τιμής ΕΚ=(-31€)*0.714+(100€)*0.1+(44€)*0.186=-3.95€